Kurze Newton Frage

[pk93]

Wie kann ich mit Hilfe von Newton die Extremwerte einer Funktion ausrechnen? Die NSt's hab ich schon.

Hoffe ihr könnt mir helfen.

Lg
pk93

[Giga]

x Index n+1 (xn+1) = xn- f(xn)/f'(xn)

xn wählst du beliebig, aber nicht als Definitionslücke von f(x). Damit findet man Nullstellen... aber damit ein bisschen Arbeit auch bei dir liegt, kannst du dir selbst überlegen, wie man damit Extremstellen findet.

[drancer]

http://de.wikipedia.org/wiki/Differentialrechnung (falls jemand genauer nachlesen will)

Die Extremstellen einer Funktion errechnet man mithilfe der ersten Ableitung.
f '(x) = 0
falls f ''(x) < 0 -> lokales Maximum
falls f ''(x) > 0 -> lokales Minimum

Die Ableitungen sollte man sich selbst ausrechnen können...

@Giga: mit deinem kann ich überhaupt nichts anfangen ^^

[Giga]

*gg* Mag sein, aber das was ich geschrieben habe ist das, was man "Newton-Verfahren" nennt.. ist sehr hilfreich bei Funktionen, bei denen man ansonsten eben nicht die Nullstellen finden würde (oder nur mit sehr viel Aufwand). Was du sagst, ist zwar richtig und sicher hilfreich für Funktionen wie x³-x², aber das Newton-Verfahren kann man auf praktisch alles loslassen und er fragt ja explizit nach einer Lösung durch Newton.

[drancer]

Du hast recht, damit findet man Nullstellen, aber ich sehe nicht wie das dem TE helfen soll, der schon die Nullstellen von f(x) ausgerechnet hat. Er wird sicher keine Aufgabe bekommen, welche über Polynome des 3ten Grades herausgehen, außerdem möchte er wissen wie er die Extremstellen berechnet, welche er über das Newtonverfahren nicht erhält.
Abgesehen geht die Differentialrechnung auf Leibniz und Newton zurück, "nach Newton" würde ich also auch diese Methode auffassen.

[Giga]

Na, ich hab doch schon im ersten Post geschrieben, dass er ein wenig eigene Denkleistung da reinstecken sollte, wie man mit dem Newton-Verfahren zur Nullstellenfindung Extremstellen findet.
Dass die Differentialrechnung zum Teil auf Newton zurückzuführen ist, ist mir bewusst - aber wenn man von Extremwertfindung durch Newton redet, meint man im allgemeinen das nach Newton benannte Verfahren.

Im Übrigen geht es weniger darum, dass die Polynome über den Grad 3 hinausgehen, sondern vielmehr um die Art, wie die Gleichung sich präsentiert - nehmen wir einfach 2^x - x² +3=0.

[drazzer]

Wendest das Newton-Verfahren auf die Ableitung an, weil die Nullstellen der Ableitung sind bekanntermaßen die Extremwerte der Funktion.

@die anderen: Man kann's auch komplizierter machen, als es ist. Es wird nämlich genau dadurch kompliziert, dass ihr irgendwelche Beispiele und Formeln verwendet. Ich denke, der TE weiss, wie man das Newton-Verfahren anwendet, von daher reicht ein einfacher erklärender Satz aus, und er muss Denkarbeit reinstecken

[pk93]

falls ihr es wissen sollt es geht um y=x*cos(x)

xn f(xn) f'(xn) xn+1
PI/2 cos(x)-x*sin(x) -2sin(x)-x*cos(x) xn-f(xn)/f'(xn)

dann xn-1 in f(xn) einsetzen.
ist der Extremwert? Hab ich das richtig verstanden?
oder wie ist das gemeint

[Giga]

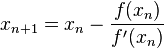
Damit man sich besser versteht^^ Du setzt im Prinzip eine beliebigen Wert für xn ein und berechnest damit xn+1. xn+1 setzt du dann als neues xn ein und so weiter. Das Verfahren konvergiert im allgemeinen gegen die Nullstelle von f(x), die am nächsten an deiner gewählten Zahl dran liegt.

[pk93]

ist mir jetzt klar mit den EW's.

thx an alle.

kann geschlossen werden

[Mr. J:J]

falls ihr es wissen sollt es geht um y=x*cos(x)

Das schreit nach der Produktregel oder?

Demnach wäre die 1.Ableitung:

f´(x)= x*sin(x)+ 1*cos(x)

Für Extremstellen gilt:
notwendige Bedingung: f´(x)= 0 = x*sin(x)+cos(x)


E/
Hab mir das mal in Derive6 angeschaut und komme zu dem Ergebnis das du nicht glücklich werden wirst xD
Du hast unendlich viele Extrema und der Funktionswert steigt ja auch stetig an....die genaue Aufgabenstellung wäre hilfreich.

[pk93]

@Mr. J:J

Die NSt waren kein Problem nur die Überlegung zu den Extremwerten

1. Ableitung ist außerdem cos(x) - x*sin(x)


hab ich schon geschafft.

Ist eig. ganz logisch, hatte nur immer einen falschen Denkansatz^^

edit: ich muss nur bis 4*Pi also nur 4 EWs

[Jimi Hendrix]

"unendlich viele extrema" ...natürlich, ist ja ne periodische Funktion ;D

[Mr. J:J]

1. Ableitung ist außerdem cos(x) - x*sin(x)

wo kommt dein minus her o.O

Die Produktregel ist doch :

f´(f*g)=f´*g + f*g´

x*cos(x)--> Abl: von x = 1 und von cos = sin

1*cos(x) + x*sin(x)

wo kommt da ein minus her?

[Andi90]

Die Ableitung von cos(x) ist -sin(x)